How to Calculate R Correlation Coefficient: A Clear and Knowledgeable Guide
Calculating the correlation coefficient (r) is a fundamental statistical concept that is used to measure the strength and direction of the relationship between two variables. The correlation coefficient can take on values between -1 and 1, where a value of -1 indicates a perfect negative correlation, a value of 0 indicates no correlation, and a value of 1 indicates a perfect positive correlation. Understanding how to calculate the correlation coefficient is essential for anyone working with data, as it can provide insights into the relationships between variables and help identify patterns and trends.
To calculate the correlation coefficient, several methods can be used, including the Pearson correlation coefficient, the Kendall correlation coefficient, and the Spearman correlation coefficient. The Pearson correlation coefficient is the most commonly used method and is used to measure the linear relationship between two variables. The Kendall correlation coefficient is used to measure the strength of the relationship between two variables when the data is ranked, and the Spearman correlation coefficient is used to measure the strength of the relationship between two variables when the data is not normally distributed.
In this article, we will explore how to calculate the correlation coefficient using different methods and provide examples of how to interpret the results. By the end of the article, readers will have a clear understanding of how to calculate the correlation coefficient and how to use it to gain insights into the relationships between variables.
Understanding Correlation
Definition of Correlation
Correlation is a statistical measure that describes the relationship between two or more variables. It is a way to determine how closely related two variables are. A correlation coefficient is a measure of the strength and direction of the relationship between two variables. The correlation coefficient is represented by the letter “r”.
Types of Correlation
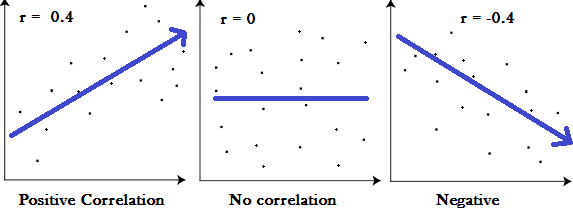
There are three types of correlation: positive, negative, and zero. A positive correlation means that two variables increase or decrease together. A negative correlation means that as one variable increases, the other variable decreases. A zero correlation means that there is no relationship between the two variables.
It is important to note that correlation does not imply causation. Just because two variables are correlated, it does not mean that one variable causes the other. There may be other factors that are causing the relationship between the two variables.
In summary, correlation is a statistical measure that describes the relationship between two or more variables. There are three types of correlation: positive, negative, and zero. It is important to understand that correlation does not imply causation.
The Concept of R Correlation Coefficient
The R correlation coefficient is a statistical measure that determines the strength and direction of the relationship between two variables. It is a value between -1 and 1, where -1 indicates a perfect negative correlation, 0 indicates no correlation, and 1 indicates a perfect positive correlation. The R correlation coefficient is widely used in various fields, including finance, social sciences, and engineering.
Pearson’s R
Pearson’s R is the most common type of R correlation coefficient used in statistics. It measures the linear relationship between two continuous variables. Pearson’s R is calculated by dividing the covariance of the two variables by the product of their standard deviations. A positive Pearson’s R indicates a positive correlation, while a negative Pearson’s R indicates a negative correlation.
Spearman’s Rho
Spearman’s Rho is a non-parametric version of the R correlation coefficient. It measures the monotonic relationship between two continuous or ordinal variables. Spearman’s Rho is calculated by ranking the two variables and then calculating Pearson’s R on the ranks. Spearman’s Rho is used when the data is not normally distributed or when outliers are present.
Kendall’s Tau
Kendall’s Tau is another non-parametric version of the R correlation coefficient. It measures the ordinal relationship between two variables. Kendall’s Tau is calculated by counting the number of concordant pairs and discordant pairs in the data. Kendall’s Tau is used when the data is not normally distributed or when outliers are present.
In summary, the R correlation coefficient is a valuable statistical tool for determining the strength and direction of the relationship between two variables. Pearson’s R, Spearman’s Rho, and Kendall’s Tau are different types of R correlation coefficients that are used in different situations.
Data Collection and Preparation
Before calculating the r correlation coefficient, it is essential to collect and prepare the data properly. The following steps can help ensure that the data is suitable for calculating the r correlation coefficient:
Step 1: Define the Variables of Interest
The first step in collecting data is to define the variables of interest. The variables should be clearly defined and measurable. For example, if the study aims to determine the relationship between a person’s height and weight, then height and weight are the variables of interest.
Step 2: Collect the Data
The second step is to collect the data. The data can be collected using various methods such as surveys, questionnaires, and experiments. It is important to ensure that the data collected is accurate and reliable.
Step 3: Check for Outliers
Outliers are data points that are significantly different from other data points. Outliers can affect the r correlation coefficient and should be checked for and removed if necessary.
Step 4: Check for Normality
The r correlation coefficient assumes that the data is normally distributed. Therefore, it is important to check for normality using methods such as a histogram or a normal probability plot.
Step 5: Check for Linearity
The r correlation coefficient measures the linear relationship between two variables. Therefore, it is important to check for linearity using methods such as a scatterplot.
By following these steps, the data can be properly collected and prepared for calculating the r correlation coefficient.
Calculating the R Correlation Coefficient
Formula Explanation
The R correlation coefficient measures the strength and direction of the linear relationship between two variables. It ranges from -1 to 1, where -1 indicates a perfect negative correlation, 0 indicates no correlation, and 1 indicates a perfect positive correlation. The formula to calculate the R correlation coefficient is:
Where:
- x̄ is the mean of the first variable
- ȳ is the mean of the second variable
- xi and yi are individual values from the two variables
- n is the number of values in the sample
Step-by-Step Calculation
To calculate the R correlation coefficient manually, follow these steps:
- Compute the mean of the first variable (x̄) and the mean of the second variable (ȳ).
- For each value in the two variables, subtract the mean of the respective variable.
- Multiply the differences obtained in step 2 for each pair of values and sum them up.
- Divide the sum obtained in step 3 by (n-1) times the standard deviation of the first variable times the standard deviation of the second variable.
- The result is the R correlation coefficient.
Using Statistical Software
Statistical software can easily calculate the R correlation coefficient for you. For example, in R, you can use the cor() function to calculate the R correlation coefficient between two variables. The function takes two arguments, the first variable and the second variable. You can also specify the method to use for the calculation, such as Pearson, Spearman, or Kendall.
In Python, you can use the corr() method from the Pandas library to calculate the R correlation coefficient. The method takes the two variables as arguments and returns the R correlation coefficient.
Overall, calculating the R correlation coefficient can be done manually using the formula or with the help of statistical software. Knowing how to calculate the R correlation coefficient is important for understanding the relationship between two variables and making informed decisions based on data analysis.
Interpreting the Results
Coefficient Value Meaning
After calculating the Pearson correlation coefficient (r), it is important to interpret its value. The value of r ranges from -1 to 1, where -1 indicates a perfect negative correlation, 0 indicates no correlation, and 1 indicates a perfect positive correlation. A correlation coefficient of 0.5, for example, indicates a moderate positive correlation, while a coefficient of -0.7 indicates a strong negative correlation.
It is important to note that correlation does not imply causation. A high correlation between two variables does not necessarily mean that one variable causes the other. It is possible that the correlation is due to a third variable that affects both variables being studied.
Statistical Significance
In addition to interpreting the value of r, it is also important to determine whether the correlation coefficient is statistically significant. Statistical significance indicates whether the correlation observed in the sample is likely to exist in the population.
To determine statistical significance, a hypothesis test can be conducted. The null hypothesis is that there is no correlation between the two variables in the population. The alternative hypothesis is that there is a correlation.
If the p-value is less than the significance level (usually 0.05), the null hypothesis is rejected, indicating that there is a statistically significant correlation between the two variables. If the p-value is greater than the significance level, the null hypothesis is not rejected, indicating that there is no statistically significant correlation between the two variables.
In conclusion, interpreting the results of the Pearson correlation coefficient involves determining the meaning of the coefficient value and determining whether the correlation is statistically significant.
Assumptions and Limitations
Normality
The Pearson correlation coefficient assumes that both variables being analyzed are normally distributed. Normality means that the data follows a normal distribution, which is a bell-shaped curve. If the data is not normally distributed, the correlation coefficient may not accurately reflect the strength and direction of the relationship between the variables. To check for normality, the researcher can use a normal probability plot or a histogram. If the data is not normally distributed, the researcher can use a transformation to make the data more normal.
Linearity
The Pearson correlation coefficient assumes that the relationship between the two variables is linear. A linear relationship means that as one variable increases, the other variable increases or decreases at a constant rate. If the relationship between the variables is not linear, the correlation coefficient may not accurately reflect the strength and direction of the relationship. To check for linearity, the researcher can use a scatter plot. If the scatter plot shows a curved relationship, the researcher can use a transformation to make the relationship more linear.
Homoscedasticity
The Pearson correlation coefficient assumes that the variance of the residuals is constant across all levels of the independent variable. Homoscedasticity means that the spread of the residuals is the same for all levels of the independent variable. If the variance of the residuals is not constant, the correlation coefficient may not accurately reflect the strength and direction of the relationship between the variables. To check for homoscedasticity, the researcher can use a scatter plot. If the scatter plot shows a funnel shape, the researcher can use a transformation to make the spread of the residuals more constant.
It is important to note that the Pearson correlation coefficient only measures the strength and direction of a linear relationship between two variables. It does not measure causation or the strength and direction of a non-linear relationship. Additionally, the Pearson correlation coefficient is sensitive to outliers and can be affected by the range of values of the variables being analyzed. Therefore, it is important to interpret the results of the correlation coefficient with caution and to consider the assumptions and limitations of the analysis.
Testing the Validity of the R Coefficient
After calculating the r correlation coefficient, it is important to test its validity. This can be done by performing a hypothesis test to determine whether the correlation coefficient is statistically significant or not.
The formula for the test statistic is t = r√n − 2 √1 − r2, where t is the test statistic, r is the correlation coefficient, and n is the sample size. The value of the test statistic, t, is shown in the computer or massachusetts mortgage calculator output along with the p-value. The test statistic t has the same sign as the correlation coefficient r. The p-value is the combined area in both tails.
If the p-value is less than the level of significance (usually 0.05), then the correlation coefficient is statistically significant, and it can be concluded that there is a significant linear relationship between the two variables. On the other hand, if the p-value is greater than the level of significance, then the correlation coefficient is not statistically significant, and it can be concluded that there is no significant linear relationship between the two variables.
It is important to note that a statistically significant correlation coefficient does not necessarily imply causation. There may be other variables that are affecting the relationship between the two variables being studied. Therefore, it is important to consider other factors when interpreting the results of a correlation analysis.
In summary, testing the validity of the r correlation coefficient is an important step in analyzing the relationship between two variables. By performing a hypothesis test, one can determine whether the correlation coefficient is statistically significant or not, and draw conclusions about the linear relationship between the two variables.
Reporting the Findings
Once the r correlation coefficient has been calculated, it is important to report the findings in a clear and concise manner. The following guidelines should be followed when reporting the findings:
Use APA Format
When reporting the r correlation coefficient, it is important to use the APA format. This includes reporting the value of the correlation coefficient, the degrees of freedom, and the p-value. The p-value should be rounded to three decimal places, while the value of the correlation coefficient should be rounded to two decimal places. The leading zero should be dropped for both the p-value and the correlation coefficient.
Interpret the Results
When reporting the findings, it is important to interpret the results in a way that is easy for the reader to understand. The interpretation should include the direction and strength of the relationship between the two variables. A positive correlation indicates that as one variable increases, the other variable also increases. A negative correlation indicates that as one variable increases, the other variable decreases. The strength of the correlation can range from weak to strong, with a correlation coefficient of 1 indicating a perfect positive correlation and a correlation coefficient of -1 indicating a perfect negative correlation.
Use Visual Aids
Visual aids such as tables and graphs can be used to help convey the findings in a clear and concise manner. Tables can be used to report the correlation coefficients for multiple variables, while graphs can be used to show the relationship between the variables. When using visual aids, it is important to ensure that they are easy to read and understand. Labels should be clear and concise, and the scale should be appropriate for the data being presented.
By following these guidelines, the findings of the r correlation coefficient can be reported in a clear and concise manner that is easy for the reader to understand.
Frequently Asked Questions
What steps are involved in calculating the correlation coefficient by hand?
To calculate the correlation coefficient by hand, you need to follow these steps:
- Calculate the mean of the x-values and the y-values.
- Calculate the standard deviation of the x-values and the y-values.
- Calculate the covariance of the x-values and the y-values.
- Divide the covariance by the product of the standard deviations of x and y to get the correlation coefficient.
How can you determine the correlation coefficient using Excel?
To determine the correlation coefficient using Excel, you can use the CORREL function. This function takes two arrays of values as inputs and returns the correlation coefficient between them. The syntax for the CORREL function is:
=CORREL(array1, array2)
What is the process for interpreting the strength of a correlation coefficient?
The strength of a correlation coefficient can be interpreted as follows:
- A correlation coefficient of 1 indicates a perfect positive correlation.
- A correlation coefficient of -1 indicates a perfect negative correlation.
- A correlation coefficient of 0 indicates no correlation.
- The closer the correlation coefficient is to 1 or -1, the stronger the correlation.
Which formula is used for computing the sample correlation coefficient?
The formula used for computing the sample correlation coefficient is:
r = (nΣxy - ΣxΣy) / sqrt((nΣx^2 - (Σx)^2)(nΣy^2 - (Σy)^2))
where n is the sample size, Σxy is the sum of the products of the x-values and y-values, Σx and Σy are the sums of the x-values and y-values, and Σx^2 and Σy^2 are the sums of the squares of the x-values and y-values.
How do you assess the R value’s significance in correlation analysis?
To assess the significance of the correlation coefficient, you can use a hypothesis test. The null hypothesis is that there is no correlation between the two variables, and the alternative hypothesis is that there is a correlation. The test statistic is calculated as:
t = r * sqrt(n - 2) / sqrt(1 - r^2)
where n is the sample size. If the absolute value of the test statistic is greater than the critical value from the t-distribution with n-2 degrees of freedom and a chosen significance level, then the null hypothesis is rejected and it can be concluded that there is a significant correlation between the two variables.
What methods are available for calculating the correlation coefficient from summary statistics?
There are several methods available for calculating the correlation coefficient from summary statistics, including:
- Pearson correlation coefficient: This method is used when the variables are normally distributed and have a linear relationship.
- Spearman correlation coefficient: This method is used when the variables are not normally distributed or have a nonlinear relationship.
- Kendall correlation coefficient: This method is used when the variables are ranked data and have a monotonic relationship.
